Historically, capital buffers have been recognised as one of the key tools to curb systemic risk and the spillover of shocks from the financial system to the real economy (Sibert 2010, Tente and Düllmann 2013, Altunbas et al. 2017, Mendicino et al. 2021). There is, however, a large disconnect between the academic and regulatory approaches used to evaluate systemic risk. The academic approaches favour the use of market data and asset pricing methods (Huang et al. 2012, Brownlees and Engle 2017, Adrian and Brunnermeier 2016, Acharya et al. 2017). Regulators, on the other hand, rely on balance sheet and regulatory data to generate a score of systemic importance (EBA 2020).
In two recent papers, we address this gap. In the process, we bring to light the risk management role of policymakers. Using bank distress dependencies implied from the credit default swap (CDS) markets, we quantify systemic risk and attribute it to a universe of key individual banks in Europe. This allows us to evaluate the size of the socially optimal macroprudential buffers that banks need to hold. Since capital buffers are one of the main policy instruments for managing banks’ potential contributions to systemic distress, our findings have substantial implications for managing systemic risk in the European Economic Area (EEA).
Risk measurement
First, in Dimitrov and van Wijnbergen (2023a), we develop а framework for measuring systemic risk and attributing it across the universe of European banks based on an approach used in the securitisation industry to model the potential for loss in a portfolio of defaultable loans (Tarashev and Zhu 2006). In that sense, the banking system is modelled as a portfolio of loans and systemic risk measures the potential loss for the sector given that multiple institutions default at the same time.
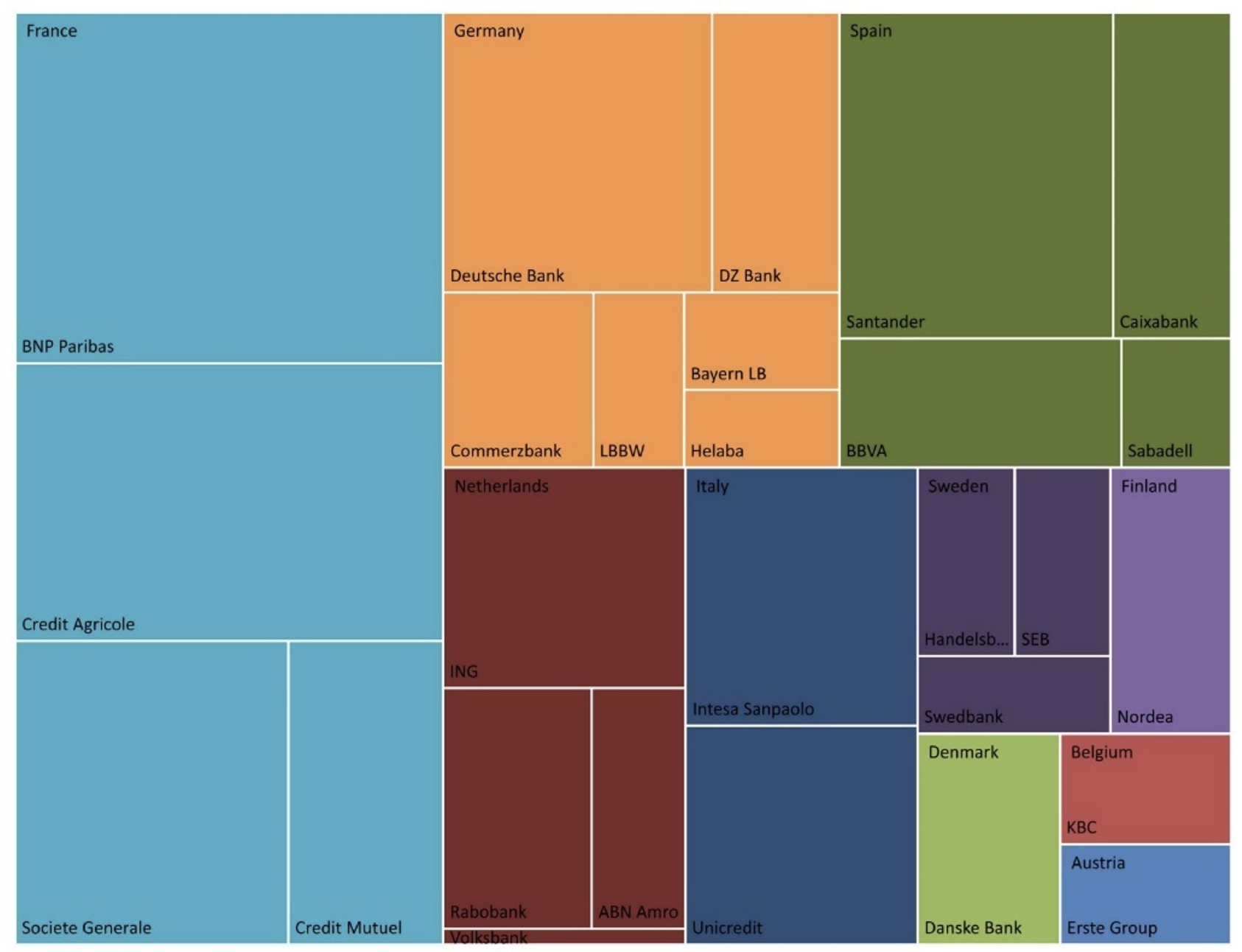
Figure 1 Banks by liability size
In both cases, we use market-driven estimates of systemic relevance. In contrast to the seminal approaches of Adrian-Brunnermeier’s CoVaR (Adrian and Brunnermeier 2016) and Acharya’s marginal expected shortfall (MES) (Acharya et al. 2017) which rely on co-dependencies in the tails of banks’ equity prices, we base our model on a credit risk model calibrated on the prices of single-name credit default swap contracts. This allows us to include in the analysis a number of banks whose equity is not publicly traded, either because they are privately held, cooperatives, or held by the government in some form. Figure 1 shows the full universe that we consider with the area of each rectangle indicating the liability size of each bank in the system.
Credit default swap prices
First, let us discuss what a credit default swap (CDS) contract is. In essence, it is an insurance, which is traded over-the-counter (OTC), and in which the protection buyer agrees to make regular payments – the CDS spread rate over a notional amount – to the protection seller. In return, the protection seller commits to compensate the buyer in case of default of the contractually referenced institution.
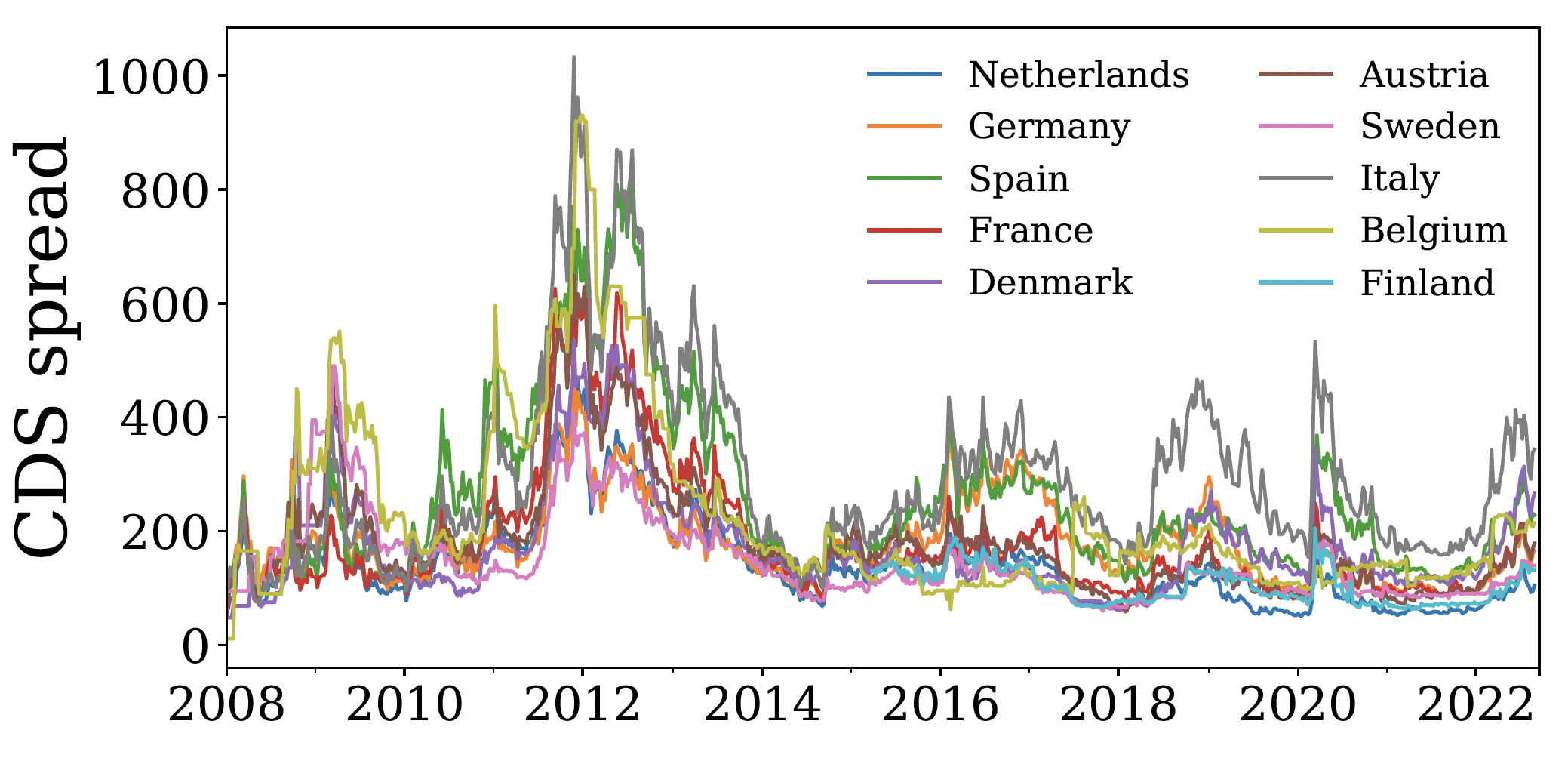
There are multiple features of the contract that make it an attractive source of information on the risks which are evolving in the financial sector: the contract directly targets risks of insolvency, it has standardised terms and conditions, better liquidity than corporate debt, a tendency to lead equity markets in price discovery, and prices in government intervention and restructuring of the reference institution. Figure 2 shows the median bank credit default swap spreads per country in our sample and gives us an initial view of the common trends affecting creditworthiness between countries.
Figure 2 Median bank credit default swap (CDS) rates per country
Implying asset correlations and common factor exposures
We can define a model of systemic risk that can be calibrated based on the observed CDS prices over time. There are several key mechanisms behind the method that we develop based on observed CDS prices.
First, we know through Merton (1974) that the market value of a company's assets is related both to the market value of its equity and of its liabilities. The level of the firm's CDS spread at any particular instance thus relates to the chance that the value of its assets may drop and that it may experience distress in the form of a credit event captured by the CDS contract.
Second, as a measure of systemic risk exposure, we look at the propensity of multiple banks to default at the same time. We rely on a Vasicek-type factor model typically used for the estimation of the risk of a portfolio of loans. In this approach, a set of common factors across all banks drives the common variation in their creditworthiness.
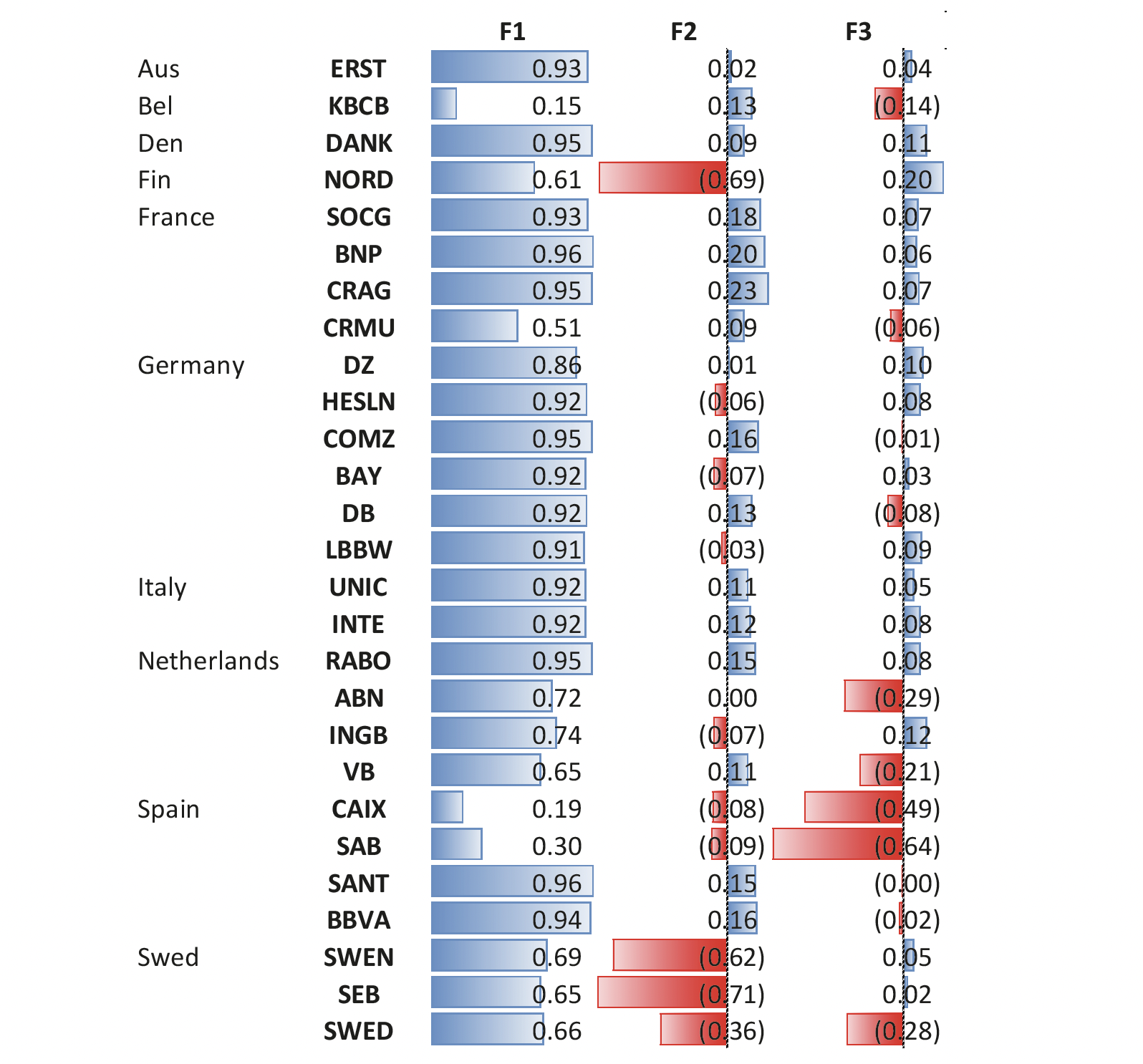
Figure 3 presents the estimated factor loadings for each bank in our universe. The clustering of exposures across banks in Figure 3 can provide some clues on the type of variation each factor may be capturing. The first factor (F1) for example seems to account for the overall market variation in the sample. All factor loadings are positive, and with few exceptions close to the upper bound of one. The other two factors capture any residual common variation with the notable clustering of similar exposures for banks from Sweden and Finland to the second factor, and for Spanish banks to the third factor.
Figure 3 Banks’ factor exposures
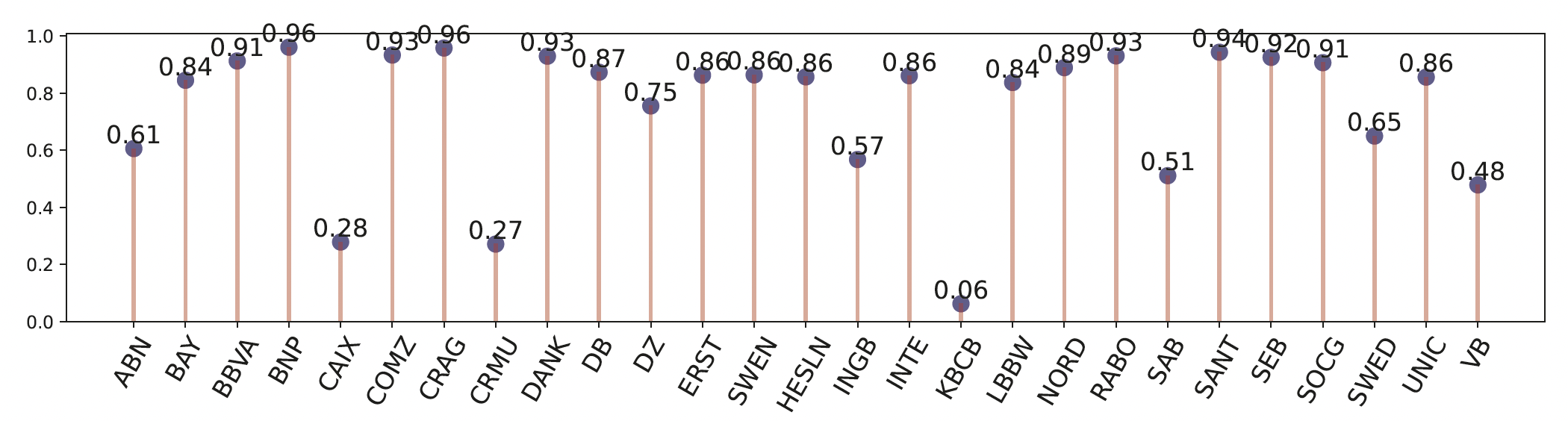
Furthermore, the individual exposure of banks to the common factors allows us to evaluate the share of total banks’ asset return variation due to common risk versus the share which is due to idiosyncratic variation unrelated to overall market conditions. Figure 4 shows the estimates for each bank in the sample. This can be seen as an initial crude estimate of the systemic sensitivity implied from the credit default swap price co-movements about an institution's assets. The higher the share of a bank's factor risk, i.e. the closer it is to one, the more its assets will tend to co-move together with the rest of the universe. The closer the share is to zero, the more the bank's risk is driven by idiosyncratic components that do not move with the rest of the universe. In our universe, the most sensitive institutions turn out to be BNP, CRAG, SANT, COMZ, and RABO.
Figure 4 Share of common factor risk
Attributing systemic risk in a cross section
The factor exposures allow us to simulate the potential default and the consequent losses of individual banks by also considering the propensity that several banks may become distressed at the same time. Weighting up the potential default losses allows us to evaluate the tail losses of the regulatory systemic portfolio. At the same time, through a measure popularised by Acharya et al. (2017) as ‘marginal expected shortfall’, we can evaluate the share of systemic risk that is attributed to each bank.
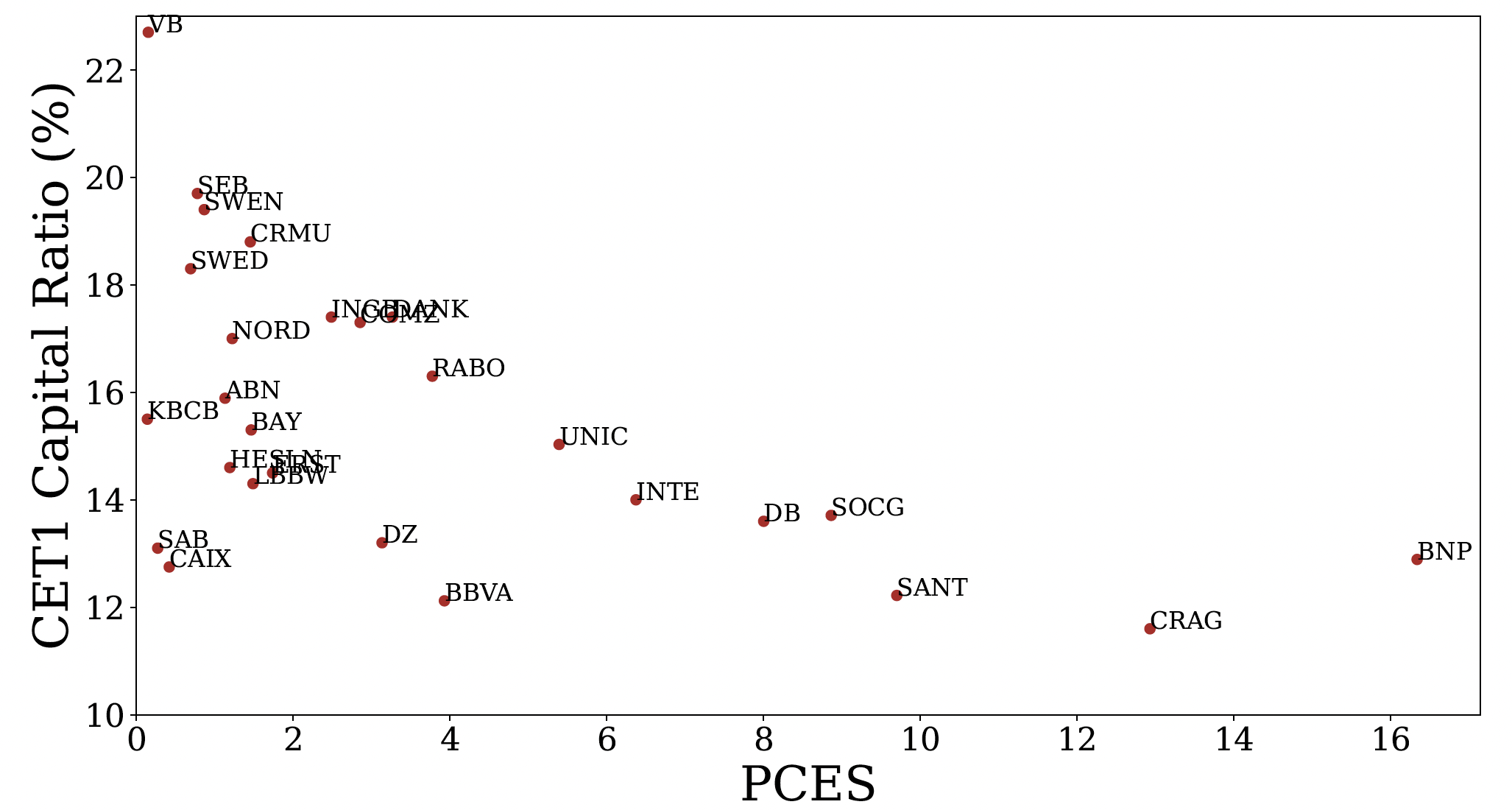
Figure 5 Percentage contribution to expected shortfall
In Figure 5 we plot the CET1 capital ratios of individual banks against the corresponding share of systemic risk attributed to the bank (PCES). The results are striking: although there seems to be a strong positive relationship between the two approaches for most banks, there is a cluster of large banks that do not fit the pattern in that their buffers seem low by comparison to the rest of the sample. The cluster is located on the right side of the chart and consists of the four largest banks in our universe, three of them domiciled in France: SOCG, CRAG, and BNP, and one domiciled in Spain: SANT. The banks located on the right side of the plot have low levels of capital compared to their contribution to systemic risk.
From risk measurement to risk management
Systemic risk measurement is directly relevant for setting the proportion of capital buffers designed to mitigate the risks that a bank's distress may pose on the financial system or the wider economy. In a policy context, the minimum capital requirements are intended to reflect and manage the risks that a bank's operations pose on its own distress. The macroprudential buffers, on the other hand, aim to improve the resilience of the financial system by internalising the systemic risks generated by an institution or the financial sector as a whole.
In Dimitrov and van Wijnbergen (2023b) we go a step further and determine the size of the macroprudential buffers that minimise the potential loss for the banking portfolio. In the process, we allow a policymaker to balance out the risks of a financial crisis when the banking sector is not well capitalised versus the risks of stifling lending and economic growth when capital requirements are raised too sharply.
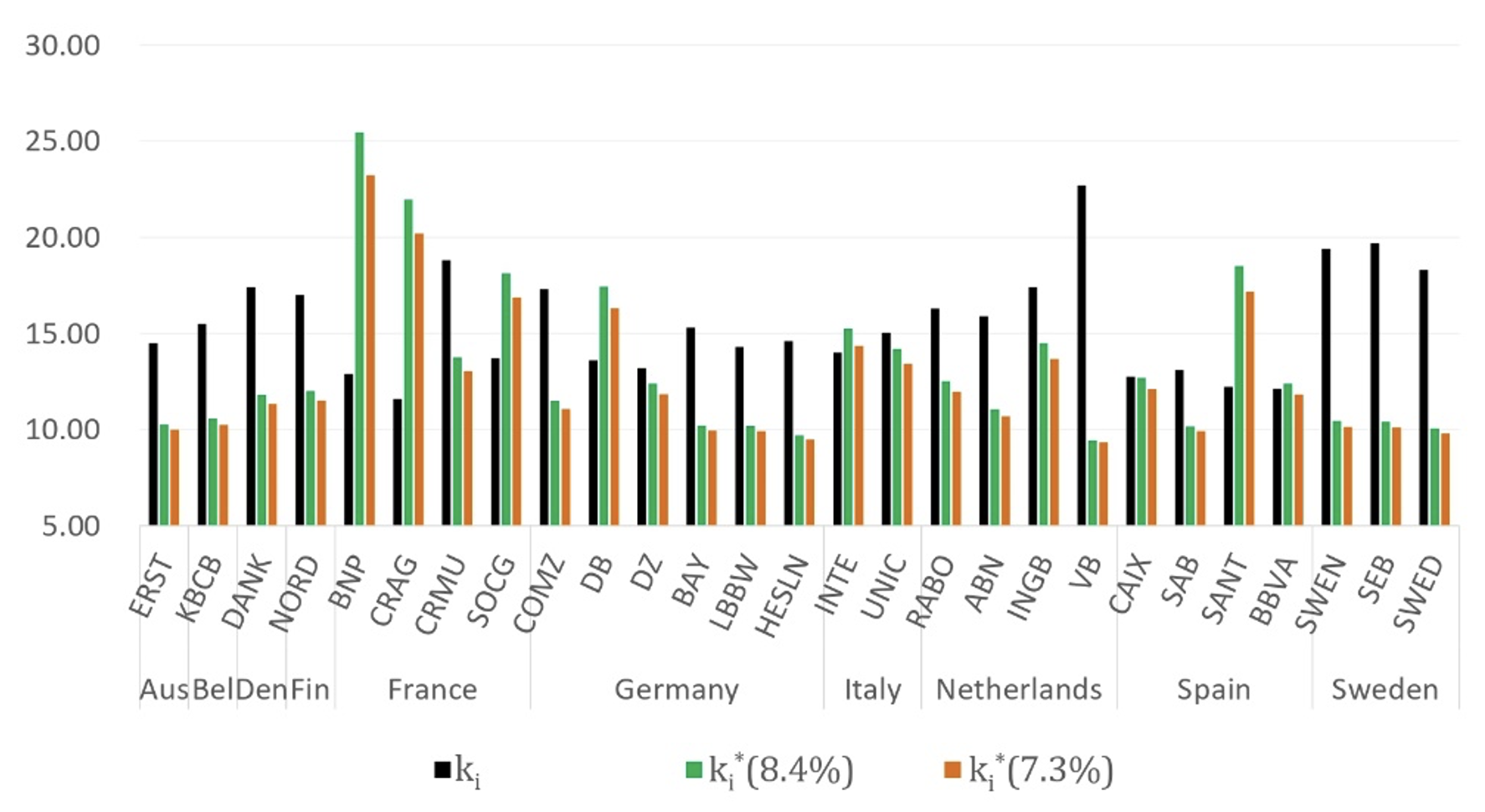
Figure 6 then shows the distribution of the socially optimal total CET1 capital based on the model, compared to the corresponding capital. Once again, we obtain similar results, with some areas where banks seem undercapitalised relative to the model recommendation and others with apparent overcapitalisation compared to the model optimum. The clearest outlier is France, where the model recommends higher capital ratios for all banks in the universe except Credit Mutuel (CRMU), a cooperative bank. The model output also indicates that Germany's Deutsche Bank (DB) and Spain's Santander (SANT) should have higher capital than they currently have. On the other hand, Dutch and Swedish banks appear with significantly higher capitalisation ratios in practice than required by the model.
Figure 6 Fully model-based optimal capital ratios (%)
Interestingly, the two Italian banks in our sample Intesa Sanpaolo (INTE) and Unicredit (UNIC) do not show a significant difference between actual and model outcomes. Even though the median spread on the Italian banks in our sample appears to be the highest compared to that of other countries throughout the evaluation period (see Figure 2), the two banks are smaller on a European scale - as Figure 1 shows, they are less than half the size of BNP, for example - which lowers the potential that they will dominate the system and thus lowers the need for larger buffer due to systemic concerns within Europe.
Authors’ note: The views expressed are those of the authors and do not necessarily reflect those of the Eurosystem or De Nederlandsche Bank.
References
Acharya, V V, L H Pedersen, T Philippon and M Richardson (2017), “Measuring systemic risk”, Review of Financial Studies 30(1): 2–47.
Adrian, T and М К Brunnermeier (2016), “CoVaR”, American Economic Review 106(7): 1705–1741.
Altunbas, Y, M Binici, L Gambacorta and A Murcia (2017), “New evidence on the effectiveness of macroprudential measures”, VoxEU.org, 5 December.
Brownlees, C and R F Engle (2017), “SRISK: A conditional capital shortfall measure of systemic risk”, Review of Financial Studies 30(1): 48–79.
Dimitrov, D and S van Wijnbergen (2023a), “Quantifying Systemic Risk in the Presence of Unlisted Banks: Application to the European Banking Sector”, De Nederlandsche Bank Working Paper No. 768.
Dimitrov, D and S van Wijnbergen (2023b), “Macroprudential Regulation: A Risk Management Approach”, De Nederlandsche Bank Working Paper No. 765.
EBA (2020), “EBA report on the appropriate methodology to calibrate O-SII buffer rates”, Policy report, European Banking Authority.
ESRB (2017), “Final report on the use of structural macroprudential instruments in the EU”, Policy report, European Systemic Risk Board.
Huang, X, H Zhou and H Zhu (2012), “Systemic risk contributions”, Journal of Financial Services Research 42(1): 55–83.
Mendicino, C, K Nikolov, J R Ramirez, J Suarez and D Supera (2021), “How much capital should banks hold?”, VoxEU.org, 24 February.
Merton, R C (1974), “On the pricing of corporate debt: The risk structure of interest rates”, Journal of Finance 29(2): 449–470.
Sibert, A (2010), “A systemic risk warning system”, VoxEU.org, 16 January.
Tarashev, N A and H Zhu (2006), “The pricing of portfolio credit risk”, BIS Working Papers 214, Bank for International Settlements.
Tente, N and K Düllmann (2013), “Macroprudential capital add-ons for systemically important banks”, VoxEU.org, 27 June.