Whether enhanced central bank transparency is favourable is not evident from the literature. For instance, the theoretical model by Morris and Shin (2002) shows that higher transparency can even have an adverse effect on the quality of private forecasts.1 They argue as follows. If central banks have only noisy information on the future evolution of some macro variables, and their noisy information is less precise than that of the market, then achieving a higher degree of transparency can crowd out valuable private information and increase the forecast error of private agents.
In contrast, the comprehensive empirical works by Ehrmann et al. (2010, 2012) claim to find support for the view that enhancing central bank transparency is favourable. Their main finding is that a higher degree of transparency is associated with significantly better private forecasts (both in the economic and statistical senses).
Let us review a couple of technical details about their results. In one of their benchmark regressions, the dependent variable is a measure of the quality of private forecasts, while the independent variable is the most commonly used measure of central bank transparency, developed by Eijffinger and Geraats (2006) (henceforth, the EG index). They estimate a dynamic panel model with country fixed effects by OLS on a sample covering advanced economies. The frequency of their sample is monthly, while the horizons of the forecasts are three months or longer, which means that the forecast horizons of consecutive forecasts are overlapping.
Should central banks become more transparent?
After taking a glance at the above results of Ehrmann et al. (2010, 2012), one might think that the answer to this question is yes. However, econometricians – and even non-econometricians – might have some doubts. There are three reasons why an econometrician would not find the above-cited empirical result to be convincing enough for the normative approach.
First, significant relationships between contemporaneous variables cannot be interpreted as evidence for causality. Second, the estimates on the parameters of a dynamic panel model with country fixed effects are biased if they are obtained with OLS. Third, overlapping forecast horizons lead to biased standard error estimates invalidating the standard t-test.
A natural question to be raised by an econometrician is whether central bank transparency proves to be favourable even after the above three issues are taken care of. An even more natural question could be asked by someone who is less familiar with econometric terms: What is the meaning of the above three points, which sound like “tohu wa-bohu” to most people?
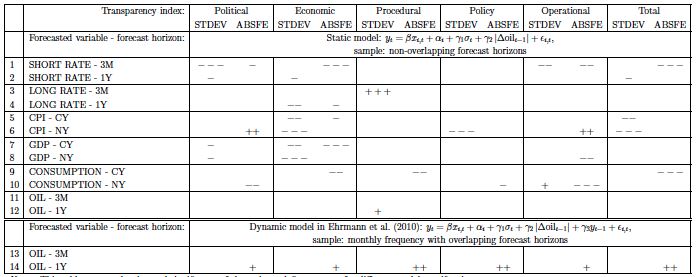
Besides our genuine interest in central banking, the intellectual challenge of answering these questions motivated our research on the topic. In recent work, one of our contributions is that we demonstrate the presence of the bias in the parameter of the transparency measure without using high-level econometrics (Naszodi et al. 2016). Here, the idea is to estimate the model not only on those variables whose forecasts are hypothesised to be influenced by central bank transparency, but also on oil price, which is exogenous to monetary policy. If estimates are unbiased, then one should not find a significant relationship between the accuracy of oil price forecasts and any measure of central bank transparency. When using the same model as Ehrmann et al. (2010), we could falsely reject exogeneity; however, we find no significant relationship between the accuracy of oil price forecasts and transparency with a more rigorous approach (see rows 11-14 in Table 1).
When using the rigorous approach, we find that different measures on transparency do have a positive association with the quality of forecasts (i.e. the forecast error is mitigated and the dispersion of views across individual forecasters is decreased) on some macro variables (rows 1-10 in Table 1). In addition, we use the Granger causality test to learn whether enhancing transparency now improves the precision of forecasts made in the future. Unfortunately, the vast majority of our tests find causality either in both directions or neither of the directions. However, in those specifications where the Granger causality points to one definite direction, it is dominantly the one that supports the normative perspective.
Table 1. Sign and significance of the estimated effect of transparency on the quality of forecasts
Notes: This table reports the sign and significance of the estimated β parameter capturing the effect of transparency on the quality of forecasts for different model specifications. Each row corresponds to a set of specifications, where the forecasted variable and the forecast horizon are identical. The forecast horizons are abbreviated as follows: 3M = 3 month, 1Y = 1 year, CY = current year, NY = next year. Each column corresponds to a set of specifications, where the transparency is captured by the same sub-index of the EG index or the composite EG index and the forecast is characterised either by the absolute forecast error of the consensus forecast (ABSFE), or by the standard deviation of the individual forecasts (STDEV). Although not reported here, further results on the effects of the 15 components of the EG index can be found in Naszodi et al. (2016). -, -- and ---, indicate negative estimates at the 10%, 5% and 1% significance levels, respectively. +, ++ and + + + indicate positive estimates at the 10%, 5% and 1% significance levels, respectively. Empty cells correspond to insignificant estimates. Sample: January 1998 - December 2009, 26 countries. Regressions are estimated by OLS. The standard errors are calculated by White cross-section method that is designed to accommodate arbitrary heteroscedasticity and robust to contemporaneous correlation across countries.
Source: Naszodi et al (2016).
Which aspects of central bank transparency matter?
To answer this question, one needs to have high enough variation in all measureable aspects of transparency to identify their effects on a proxy for economic uncertainty. Fortunately, our unique data are rich enough for the identification as they cover not only some advanced countries that are broadly the same at many dimensions of transparency, but also some emerging countries. Out of the 5 components of the EG index, we find three components to be important. Based on that, we conclude that the best practice of central banking involves:
- Preparing and publishing their own forecasts;
- Providing an explicit policy rule or strategy that describes the monetary policy framework; and
- Promptly announcing policy decisions.
Is there a better measure for the overall degree of transparency than the EG index?
The composite EG index is criticised for being an equally weighted sum of its components. Even Eijffinger and Geraats (2006) share the view that the weights of the components of the composite index should be established empirically. Our research fills the gap by constructing a weighted index, the Naszodi-Csavas-Erhart-Felcser index (henceforth the NCEF index). The index we propose aggregates the same 15 components as the EG index. The weights assigned to the components are obtained from the same regression as the one used to determine which aspects of transparency matter; thus, they reflect the relative importance of the components in reducing forecast uncertainty.
Is there a better measure for the overall degree of transparency than the NCEF index?
The NCEF index, although a weighted index, is still subject to some criticisms. First, it is a linear function of 15 components that do not necessarily complement each other in a linear manner.2 Second, there are certain aspects of central bank transparency that are captured neither by the components of the EG index nor by the NCEF index. To mention just one of these aspects, neither accounts for whether detailed information is provided on the views of the individual council members. Third, while our regression method allows us to identify which aspects of transparency are effective, it does not allow us to conclude that some other newer or less employed aspects of transparency are ineffective. In other words, the NCEF index might fail to recognise the importance of any type of transparency that has only been employed recently or by only a few countries. Fourth, if lower degree of transparency is favourable or unavoidable in some rare cases, for instance when the economy is in a state of the world that is not covered by the policy rule and unexpected or extraordinary intervention is necessary,3 then our regressions – run on a sample covering mostly ‘normal’ times – might fail to serve with universally applicable guidelines for central bankers. Fifth, we are no different from other researchers who can make unintended errors and mistakes. These points call for future research on measuring central bank transparency and its effect.
Authors’ note: The views expressed here are those of the authors and do not necessarily represent those of the institutions with which they are affiliated.
References
Csavas, C, S Erhart, A Naszodi and K Pinter (2011) “Changing central bank transparency in Central and Eastern Europe during the financial crisis”, in J A Batten and P G Szilagyi (eds), The Impact of the Global Financial Crisis on Emerging Financial Markets, Emerald Group Publishing Limited.
Ehrmann, M, S Eijffinger and M Fratzscher (2010) “The role of central bank transparency for guiding private sector forecasts”, ECB Working Paper No 1146.
Ehrmann, M, S Eijffinger and M Fratzscher (2012) “The role of central bank transparency for guiding private sector forecasts”, Scandinavian Journal of Economics, 114(3): 1018–52.
Eijffinger, S C and P M Geraats (2006) “How transparent are central banks?” European Journal of Political Economy, 22(1): 1–21.
Kool, C, M Middeldorp and S Rosenkranz (2011) “Central bank transparency and the crowding out of private information in financial markets”, Journal of Money, Credit and Banking, 43(4): 765–774.
Morris, S and H S Shin (2002) “Social value of public information”, American Economic Review, 92(5): 1521–34.
Naszodi, A, C Csavas, S Erhart and D Felcser (2016) “Which aspects of central bank transparency matter? A comprehensive analysis of the effect of transparency on survey forecasts”, International Journal of Central Banking, 12(4): 147-192.
Naszodi, A, V Kvedaras and D Felcser (2017) “Detecting non-linearity in central bank transparency indices with a non-parametric method”, unpublished manuscript.
Endnotes
1 Similar to Morris and Shin (2002), Kool et al (2011) also show that greater transparency can reduce forecasting accuracy, however, the mechanism in their model is different. Their key assumption is that market participants choose to refrain from investing in private information when they can get costless guidance on future rates from the central bank’s public signal.
2 Whether an index aggregating the fifteen components by allowing non-linear relationship between them is preferable than the linear NCEF index is examined by Naszodi et al (2017).
3 In addition, the EG index measures the degree of central bank transparency imprecisely during the recent financial and economic crisis according to our argument published in an earlier paper (see Csavas et al 2011).