How do financial frictions affect the macroeconomy? The answer helps us understand the fluctuations of the business cycle, and so is important for effective policymaking to counteract regular or financial recessions. There is a lot of research into the consequences of financial frictions in different contexts (Brunnermeier et al. 2013). But there has been remarkably little attention given to how these frictions also affect nominal price rigidity, and how this might be important for aggregate fluctuations.
In recent work, we argue that the presence of financial frictions makes nominal prices in the economy more rigid by decreasing the average frequency of price changes ceteris paribus (Balleer et al. 2017). Moreover, the way financial frictions affect the economy depends on how one thinks nominal rigidities work. If we have the opinion that financial frictions affect whether (and which) firms adjust prices, inflation reacts less, and output reacts more to aggregate shocks in the presence of frictions. Given aggregate demand, this means that financial frictions make aggregate supply flatter. Financial constraints therefore influence a fundamental trade-off faced by the central bank: to raise inflation, the monetary authority would need to accept relatively stronger responses of average output.
In contrast, if we have the opinion that financial frictions do not affect whether (and which) firms adjust prices – as assumed in most macroeconomic models – aggregate supply becomes steeper in the presence of financial frictions. In this case, inflation reacts more and output less to aggregate shocks.
The cross-sectional distribution of pricing decisions
If we are to understand this better, we need to investigate the effect of financial frictions on the cross-sectional distribution of pricing decisions. We look at the IFO Business survey, which provides information about the relationship between the extensive margin of price adjustment and financial constraints in German manufacturing. Based on this, we find that the typical financially constrained firm adjusts prices significantly more often than the corresponding unconstrained firm, both upwards and downwards.
We provide a mechanism that would be consistent with these observations. We assume that firms set prices optimally, subject to a demand schedule and a financial constraint. Firms decide whether to reset prices or not given a fixed (menu) cost of price adjustment. In a world with financial frictions, the optimal reset price is higher than in a world without financial frictions, since prices below the optimal price imply rationing output, and this is very costly to the firm. As a consequence, profits are more concave in price. This leads firms to adjust prices more often, for a given initial price distribution of firms. This effect is stronger for financially constrained firms. These firms, therefore, adjust prices more often than unconstrained firms.
As in the data, financially constrained firms may be high- or low-productivity.
High-productivity (or, equivalently, high-opportunity) firms would like to decrease prices and produce more. If financial constraints are in place, financing a lot of output becomes very expensive and firms optimally decrease prices less.
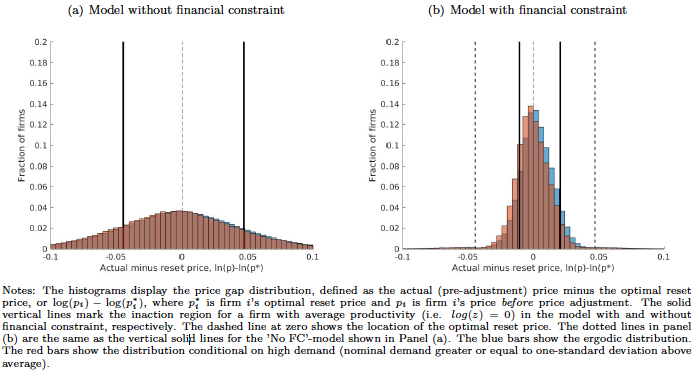
Low-productivity firms need to use and finance a lot of inputs. They therefore want to scale down production and increase prices, but not by too much in order to save future menu costs among other things. Since the optimal price change is smaller due to the financial constraint, fewer firms will adjust their prices for a given menu cost. As a consequence, the final price distribution will be more bunched around the optimal reset price (Figure 1).
Figure 1 Price distribution and positive demand shocks
Source: Balleer et al. (2017).
Aggregate implications
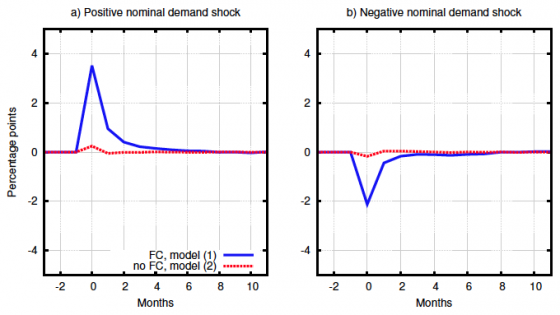
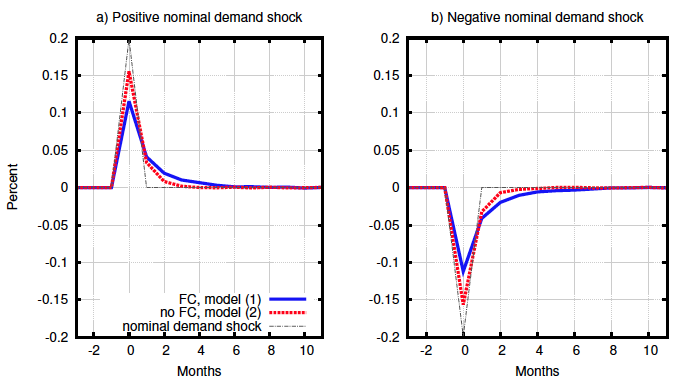
This has important implications for the economy. The distribution is more bunched when there are financial frictions, and so overall rigidities in the economy become bigger when financial constraints become tighter. Also, we modelled the effect of shocks to the aggregate price level. Individual real prices consist of the ratio of individual nominal prices and the aggregate price level. Nominal demand shocks increase the aggregate price level, and shift the aggregate price distribution (Figure 2). Due to the financial constraint, resetting prices is no longer symmetric. Not adjusting prices is costlier for lower-than-optimal prices, due to output rationing. After a positive shock, the individual real price falls if the firm does not make a nominal adjustment. Since this is very costly, there are many more firms would like to increase prices than those that no longer need to decrease prices, and so nominal rigidities decrease (Figure 2). Since the increase in individual real prices after a negative demand shock is less costly to firms, the opposite happens and nominal rigidities increase. As a result, financial frictions cause the degree of nominal price rigidity to vary over the business cycle. If nominal rigidities affect the effectiveness of monetary policy, central banks should take this into account.
Figure 2 Fraction of price changes, all firms
Source: Balleer et al. (2017).
Our mechanism implies the firms that change prices in response to aggregate shocks are not selected randomly. Rather, most firms that reset prices after a nominal demand shock would be firms with initial prices relatively close to the optimal price (since the distribution is bunched around it). When resetting their prices, these firms do not reset by large amounts, and so inflation reacts less to shocks compared to a world without financial frictions.
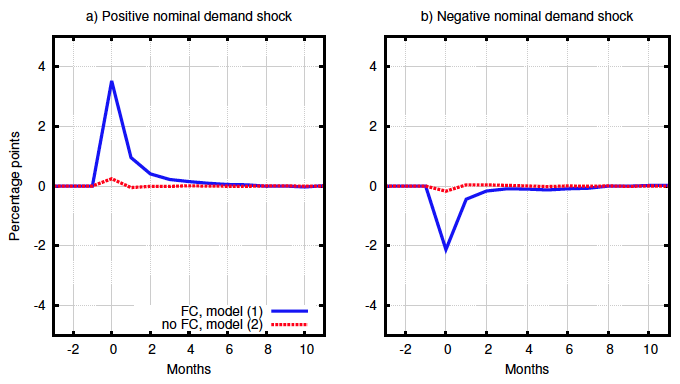
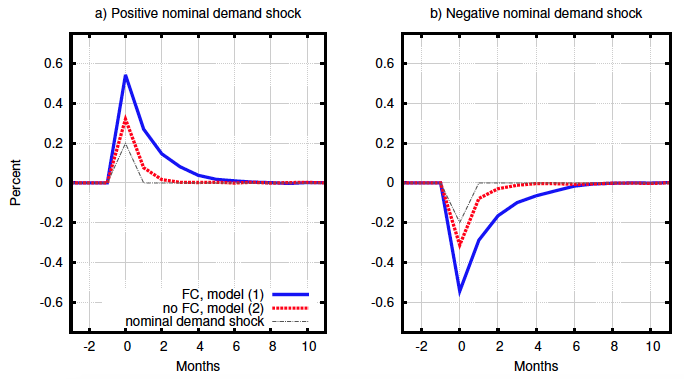
Also, output reacts more to shocks (Figure 3). In other words, aggregate shocks change the composition of price-adjusting and non-adjusting firms more strongly in the presence of financial frictions. Due to these compositional effects, aggregate shocks make the aggregate supply curve flatter, given aggregate demand. Financial frictions therefore affect the monetary policy trade-off between inflation and output.
Figure 3 Average inflation and output
a) Average prices
b) Average (real) output
Source: Balleer et al. (2017).
Why compositional effects matter
The selection channel described above is absent from most models used to study monetary policy and financial frictions. Without this selection channel, aggregate shocks have the opposite effect on the economy. They would make aggregate supply steeper. In a world with financial frictions, inflation would react in the same way (or more) and output less, compared to one without.
On one hand, one may assume that price adjustment is costly, but financial frictions affect only by how much (not whether) firms adjust prices – i.e. Rotemberg pricing (Rotemberg 1982). More precisely, financial frictions would reduce the production capacity of firms and would make firms change prices more in response to aggregate shocks than without frictions. Correspondingly, output would respond less to shocks.
On the other hand, one may assume that only a random fraction of firms reset prices every period – i.e. Calvo pricing (Calvo 1983). Since price adjustment would be independent of financial friction, the inflation response to aggregate shocks would not change. Firms that do not adjust prices would need, however, react to the financial friction by rationing output, especially after a positive demand shock. Hence output would react less to shocks than without financial frictions.
References
Balleer, A, N Hristov and D Menno (2017), “Financial Constraints and Nominal Rigidities”, CEPR Discussion Paper No. 11790. ()
Brunnermeier, M, T Eisenbach and Y Sannikov (2013), “Macroeconomics with Financial Frictions: A Survey”, in D Acemoglu, M Arellano and E Dekel (eds), Advances in Economics and Econometrics, Tenth World Congress of the Econometric Society, Vol. II: Applied Economics, Cambridge University Press, pp. 4-94.
Calvo, G A (1983), “Staggered prices in a utility-maximizing framework”, Journal of Monetary Economics (12): 383-398
Rotemberg, J J (1982), “Monopolistic Price Adjustment and Aggregate Output”, Review of Economic Studies (49): 517-531